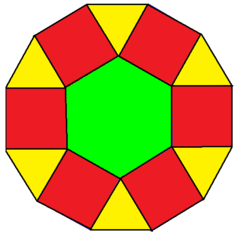
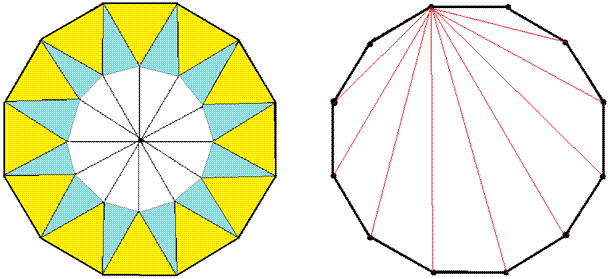
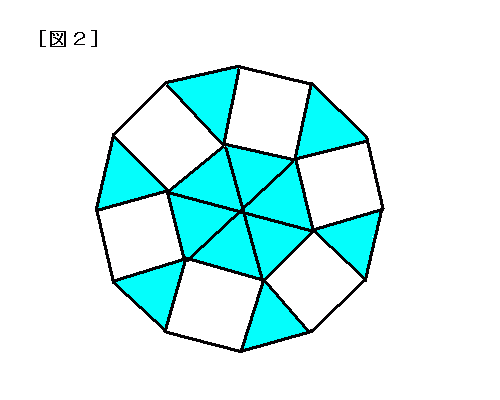
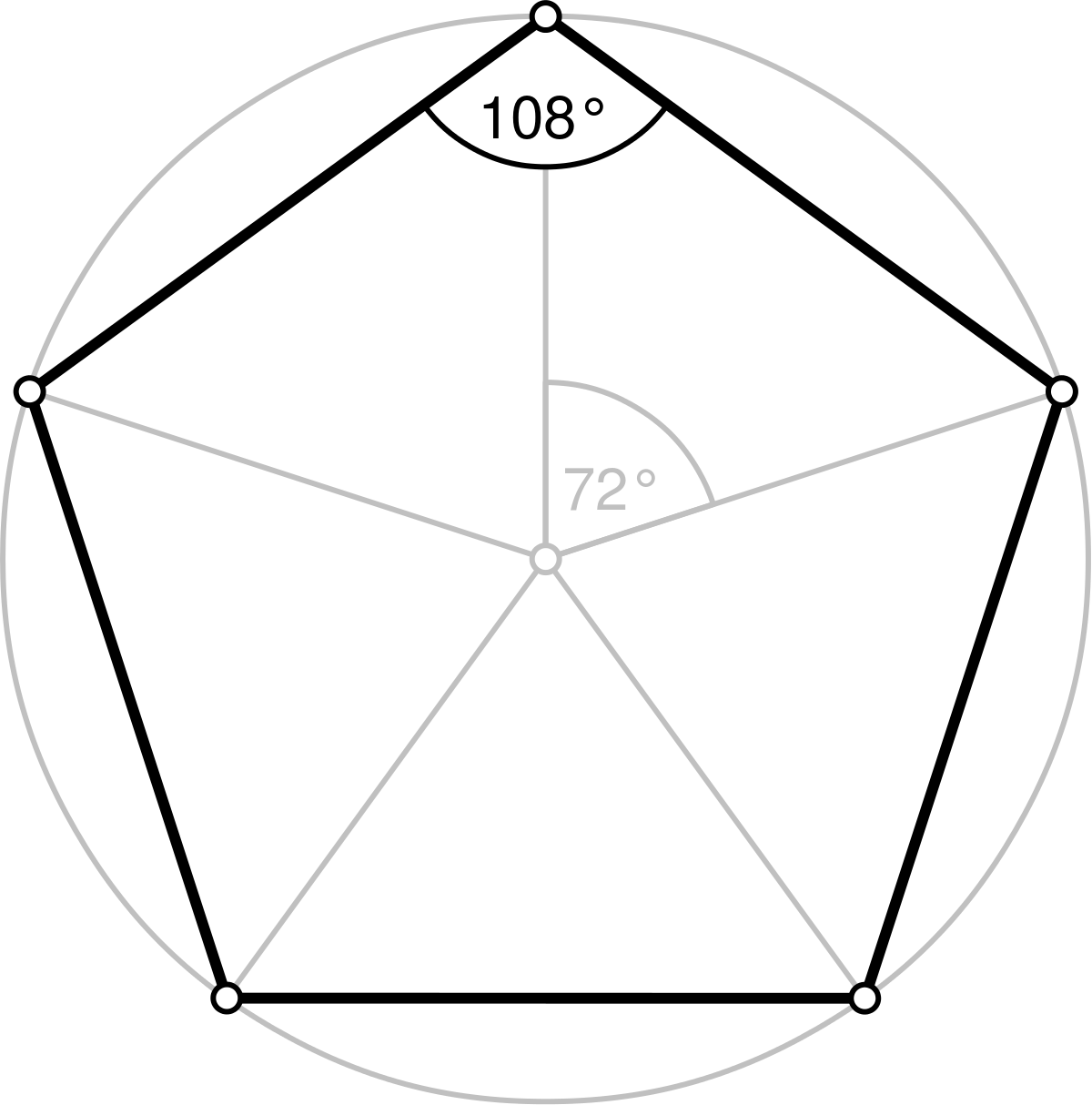
まず、12分割してひとつの三角形に注目します。 色のついた部分の面積は、全体が04cm 2 ですから、三角形一個当たり 04÷ 12= 167 04 ÷ 12 = 167 cm 22.敷きつめた正12角形 緑12 白12 白い部分の星形面積を求めよう(算数オリンピックに出題された問題) A.紙の上で考える(図を書かないで計算で) B.紙の上で考える(図を書いて)青い三角形と赤い三角形の面積の比は1:2だから, (割り切りやすいように)青い三角形の面積を6,赤い三 角形の面積を12とする。全体の面積は,6+12=18。 よって,五角形の面積は,全体の面積の となる。 ☆ ★ ☆ ★ ★ 11 18

答1474 正十二角形の対角線でできる三角形の面積 ヤドカリの 気ままな数学
正12角形 面積 公式
正12角形 面積 公式-場合のような,辺の長さと弧の長さの比較を直接使うことはできません.その代わりに面積の比較を用います. (半径1 の円の面積) < (外接する正n 角形の面積) ここで, OPiPi1 の面積は,PiPi1=2 ですから,ˇ < (外接する正n 角形の面積) = ∑n i=1 PiPi1=2 = qn=2 を 難関大学で頻出テーマの正\(n\)角形ですが、意外とその対処法を知らない受験生は多いです。この記事を読んで、その対処法を完璧にしてしまいましょう! 三角形に分割せよ 正\(n\)角形を前にしてすべきことは、ただ1つです。 Point あ 正\(n\)角形 → \(n\)個の三角形に分割 \(n\)個の三角形




16年东京大学工学系研究科系统创成学专攻 Systems Innovation システム創成学専攻 真题解析 知乎
Ⅰ 面積の公式 1辺 \\(~a~\\) の正四角形(正方形)の面積の公式は誰でも知っていますが、正三角形の面積の公式は答えられない人が多いのではないでしょうか。 しかし、正三角形は定期テストや入試でよく登場する図形であり、面積が必要となる場面も少なくありません。正n角形の1つの三角形の面積を求められると、挑戦できる問題です。 別の解き方をした人は、ぜひコメントで教えてください。 G Laboの記事でも問題を公開して正12角形は12倍すればよいから、求める面積は12 正十二角形においては、 中心角 と 外角 は30 ° で、内角は150°となる。
正 n n 角形の面積 1辺の長さが a a である正 n n 角形の面積 Sn S n は、次の公式で求められる。 Sn = na2 4tan π n S n = n a 2 4 tan 正十二角形の外角は\(360 \div 12=30°\) 正七角形や正十一角形のように $$360 \div 7=5142$$ $$360 \div 11=3272$$ 割り切れ多角形の面積 上記のような正12角形の面積を求めよという問題があったとします。 このように一見難しそうな問題であっても、三角比を用いれば簡単に求めることができます。 補助線を引く 以下のように補助線を書き、便宜的に点a、点bを決めます。正多角形の面積を求めます。 高校数学のPi/6 Ƃ ӎO p `12 D ӎO p `1 ̖ʐς́C @ @2 * (1/2) * (1/2)/tanpi/12 / 2 = (2sqrt3)/4 Ȃ̂ŁC ӂ̒ 1 ̐ \ p ` ̖ʐς @ @12 * (2sqrt3)/4 = 3 * (2sqrt3) ŁC ӂ̒ 1 ̐ O p ` ̖ʐς
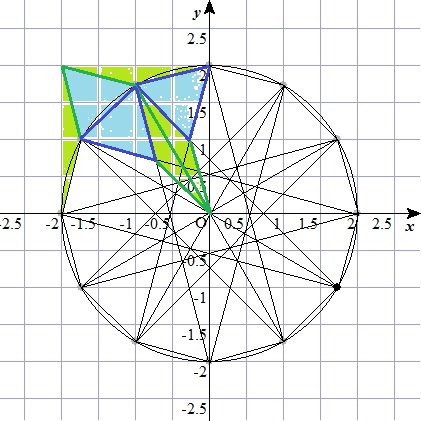
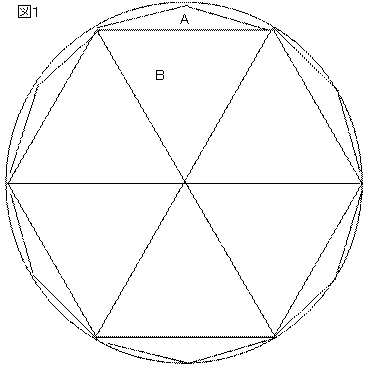
従って、半径1の円に内接する4角形, 8角形, 16角形 の面積は 円周率 \(\pi\) に近づいてゆくはずです。 図1のように、赤い4角形各辺の垂直二等分線が円に交わる点を新たな頂点として追加すれば青い8角形が得られ, 同様に各辺の垂直二等分線によって緑の16(3) 正12角形の場合 6個の台形abkl,acjl,adil,aehl,bcjk,bdikと,長方 形afgl,正方形behkについて,面積比が整数になるのは,次の通 りである。(台形,長方形,正方形の面積の計算は紙面の関係で省略 する。) (正12角形):(正方形behk):(台形adil):(長方形afgl第43問 内接する正六角形 図形ドリル 6年生 正六角形 面積比 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~! ! 」と言いそうな良問を。 受験算数の定番からマニアックな問題まで。 図形ドリルでは,色々なタイプの図形問題を取り上げ



図形 正十二角形の分解 父ちゃんが教えたるっ



Twsf Ntsec Gov Tw Activity Race 1 60 Pdf Nphsf Pdf 504
すると、このように三角形の面積も求まります。 次に、正方形の1辺の長さを考えると \(3\sqrt{2}63\sqrt{2}=66\sqrt{2}\)となるので 正方形の面積は、 $$\begin{eqnarray}(66\sqrt{2})\times (66\sqrt{2})=(66\sqrt{2})^2 \end{eqnarray}$$ となります。る正N 角形の1辺の長さを2aとすると,pN = (N 2a)=2 = Naである.一方, 図3において,OA = 1, BC = aであるから,三角形OAB の面積は, 1 2 1 a = 1 2 a である.したがって, s2N = (2N) (1 2 a) = Na = pN (1) である.すなわち,正2N 角形の面積s2N は,正N 角形の周の長さの半分pN に等正十二角形においては、 中心角 と 外角 は30 ° で、内角は150°となる。 一辺の長さが a の正十二角形の 面積 Sは




ベスト50 正12 角形 最高のぬりえ
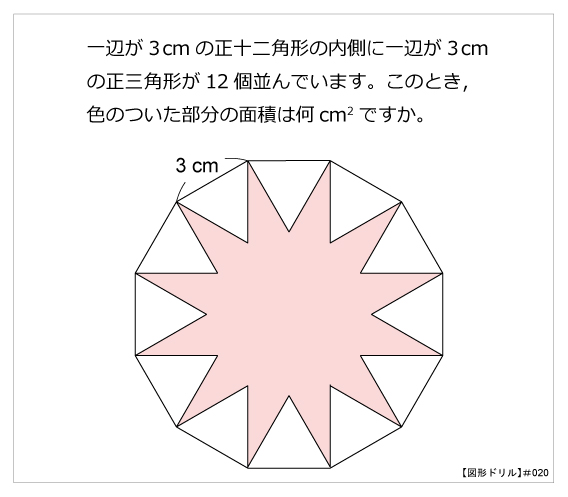



図形ドリル 第問 正十ニ角形と正三角形 算数星人のweb問題集 中学受験算数の問題に挑戦
半径2の円に内接する正十二角形の面積を求めよ。 答 12×(1/2*2sin30°)=12 なのですが、2sin30°はどういった考え方ですか?正12角形 辺の長さ 円に内接する正多角形 高精度計算サイ 使用目的 Φ600の内接する正八角形の1辺の長さを求めたかった ご意見・ご感想 円の半径r=300でのn=8の多角形の1辺の長さaはではなくて?ではないでしょうか。正12面体の体積 1辺が1の正12面体の体積を求めます。 上図は、正12面体の1つの面をxy平面上に置いた図です。 正5角形ABCDEの外接円の中心を、原点Oとし、頂点Aをχ軸上に取ります。 A:(1,0,0)と置きます。(最終的には、AB=1 となるように倍率補正します)



入試問題に挑戦第4回



正十二边形 搜狗图片搜索
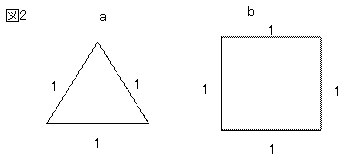
1辺の長さaが1の正三角形の面積・周囲の長さ・高さ 面積 S: 周囲の長さ L:3 高さ h:証明 2 (面積を用いた証明) 図 5: 3 <π< 4 の図 半径が r r の円と, それに内接する正十二角形,外接する正方形を図 2 に示した. ここで (正十二角形の面積) < (円の面積) < (正方形の面積) ( 正 十 二 角 形 の 面 積) < ( 円 の 面 積) < ( 正 方 形 の 面 積1辺の長さ1の正面体のそれぞれの場合の正射影の面積を求めよう. なお,以下正面体の模型を見ながら読むと分かりやすい. $\bullet \ \ $法線ベクトルが$\overrightarrow{OO_1}$のとき. 正面体を机の上に置いて真上から見ると,正射影が正6角形であることが
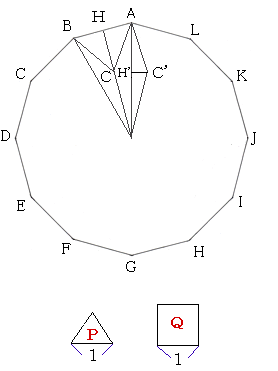



問題187 正十二角形の秘密




Woa1 Electrostatic Induction Power Generator Google Patents
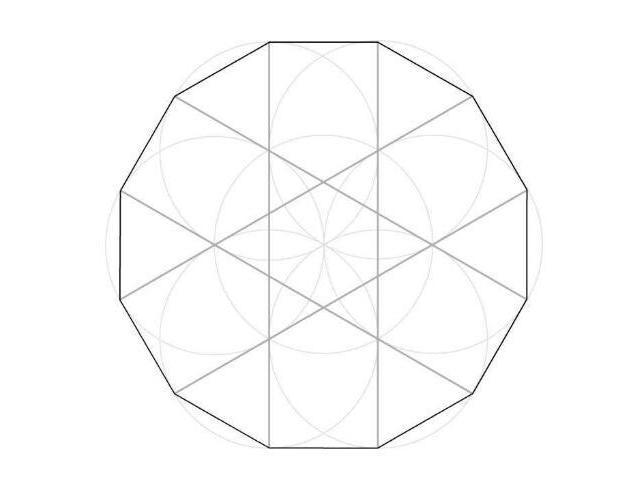
正十二角形の対角線の長さ・面積 正十二角形の 辺の長さを ,外接円の半径を ,内接円の半径を とする。 つの辺たとえば に対する弧 の中心角は ,円周角は ,正多角形の面積の公式(一般化) Fukusukeの数 算数#53正十二角形の面積 城北#平面図形 Videos von 正 十 二 角形 面積 求め 方正12角形→正24角形→正48角形→正96角形と角の数を増やしていき、角の数を増やしていく と、辺の和は円周の長さに限りなく近づいていくことから、最終的には 正96角形 を利用して、



円の中にある正十二角形の面積の求め方 半径8cmの円の内 Yahoo 知恵袋




4种方法来求六边形面积
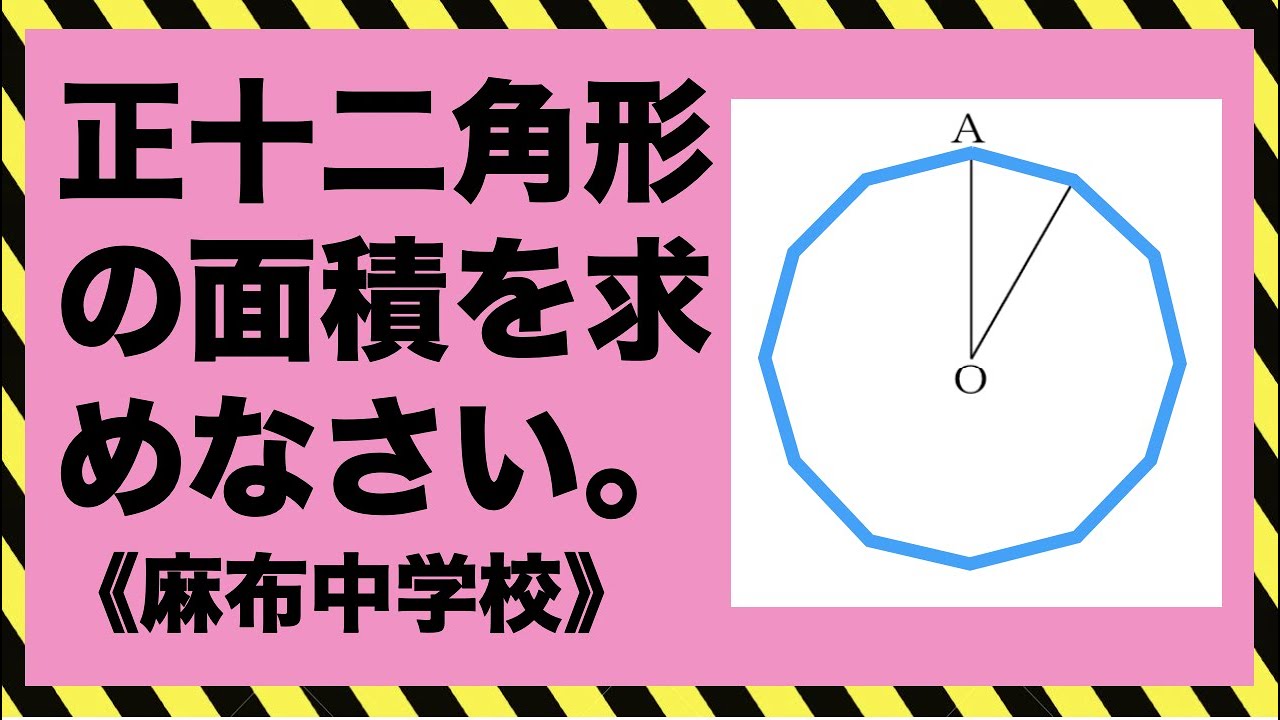
よってAC=2 AC⊥OBなので、OBを底辺としたときの△OABの高さは、ACの半分の長さにあたり、1になります。 よって、△OAB=2×1÷2=1 正十二角形は、△OABが12個あると考えればよいから、正十二角形の面積は、1×12=12 となります。 正12角形は円に内接するから、その頂角は360°/12=30°。 半径が2の2等辺三角形で、等辺を挟む角が30度の三角形の面積は、(1/2)*2*2*2*(sin30°)=1 正12角形は12倍すればよいから、求める面積は12 1 正多角形の面積 先ずは、一辺の長さがaである正n角形*1の面積を考えます。 図1 正多角形の一部を構成する二等辺三角形 正n角形は、その中心から各頂点に引いた線分によってn個の二等辺三角形に分割されたます。




多角形の面積を 三角比を用いて求める場合 数学i By Okボーイ マナペディア




十二边形 维基百科 自由的百科全书
正十二角形の面積の求め方 図は正十二角形で、Oはその中心です。 図のように1つの頂点をAとするとき、OAの長さは3cmです。 この正十二角形の面積は何c㎡ですか? スマートホンアプリ「立方体の切り口はどんな形? 」 (ネット環境でのFlashさらに ではなく を使って表すと 正 角形の面積では正 角形の面積を求めましょう。 12角形の面積 12角形の面積 左図のように、半径Rの円Oがあり、 その中に内接する正12角形の面積を考えました。 つまり ABOは、30°、60°、90°という3つの角で構成された直角三角形であることがわかります。 この直角三角形は、三辺の比が : : になる特別な図形です。 そのため、 高さは 。 面積は当然、底辺×高さ× で求められるので、以下の通りです。 = = こうした一般的な解き方でも1分以内に解答したいところですが、今回教える2大公式によって高さ2秒、面積3秒




算数 116 正十二角形の面積を求める 香蘭 平面図形 Youtube



図形 正十二角形の分解 父ちゃんが教えたるっ



正多边形十二角八角形png图片素材免费下载 图片编号 Png素材网



1




兩個小學生的12邊形燒腦題 每日頭條




問題187 正十二角形の秘密




16年东京大学工学系研究科系统创成学专攻 Systems Innovation システム創成学専攻 真题解析 知乎



12边形 万图壁纸网



入試問題に挑戦第4回




十二边形 维基百科 自由的百科全书




麻布中学校 算数 正十二角形 面積 図形問題 中学受験算数 Youtube



正十二边形内角度数 搜狗搜索




兩個小學生的12邊形燒腦題 每日頭條




十二边形 Wikiwand



十二边形 Wikiwand



最も長い対角線の長さが24cmの正12角形の面積を求めなさい Yahoo 知恵袋



正12 角形 ニスヌーピー壁紙



図形 正十二角形の分解 父ちゃんが教えたるっ




正12 角形 ニスヌーピー壁紙




ベスト50 正12 角形 最高のぬりえ



五边形 维基百科 自由的百科全书



1



正五边形 腾讯视频



入試問題に挑戦第4回



Www Shs Edu Tw Works Essay 21 03 Pdf



問題187 正十二角形の秘密




十二边形 Wikiwand



正12角形の面積 半径2の円に内接する正12角形の面積を求 Yahoo 知恵袋




例題 正三角形的高與面積 畢氏定理 均一教育平台



十二边形 Wikiwand



1




つくばサイエンスエッジ18 文京学院大学女子高校 みらいぶ 高校生サイト




ベスト50 正12 角形 最高のぬりえ




答1474 正十二角形の対角線でできる三角形の面積 ヤドカリの 気ままな数学



半径2 の円に内接する正十二角形の面積を教えて下さい 内 Yahoo 知恵袋



正12 角形 ニスヌーピー壁紙




正六角形的面積 英 多角形 四邊形與平行四邊形 均一教育平台



十二边形 搜狗百科



Ap7kf6ws E2yhm



正12 角形 ニスヌーピー壁紙




算数 53 正十二角形の面積 城北 平面図形 Youtube



問題187 正十二角形の秘密




六角形面積公式正六邊形面積公式 百度知道翻譯此網頁 Juliech



問題187 正十二角形の秘密



図形 正十二角形の分解 父ちゃんが教えたるっ




つくばサイエンスエッジ18 文京学院大学女子高校 みらいぶ 高校生サイト




三角形 21 直角三角形面積的基本計算題 Youtube



正12 角形 ニスヌーピー壁紙
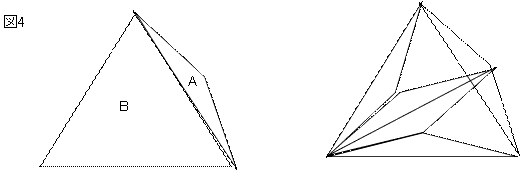



問題187 正十二角形の秘密



1
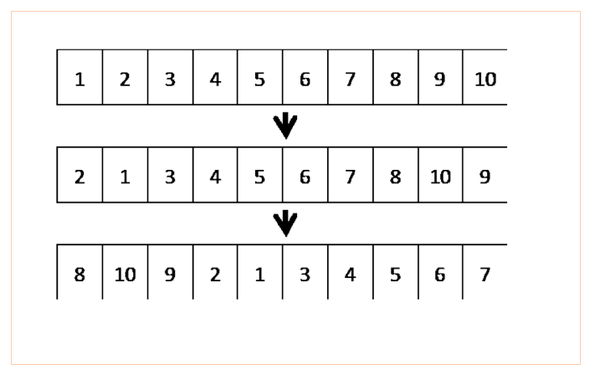



16年东京大学工学系研究科系统创成学专攻真题解析 知乎




答1474 正十二角形の対角線でできる三角形の面積 ヤドカリの 気ままな数学




Tarcy 3 Cm 0 12 Descubre Como Resolverlo En Qanda




如何求正多边形的面积 7 步骤




16年东京大学工学系研究科系统创成学专攻真题解析 知乎




問題154 正十二角形の問題




如何求正多边形的面积 7 步骤




例題 正三角形求面積 Youtube




4种方法来求六边形面积



12边形 万图壁纸网



12边形 万图壁纸网
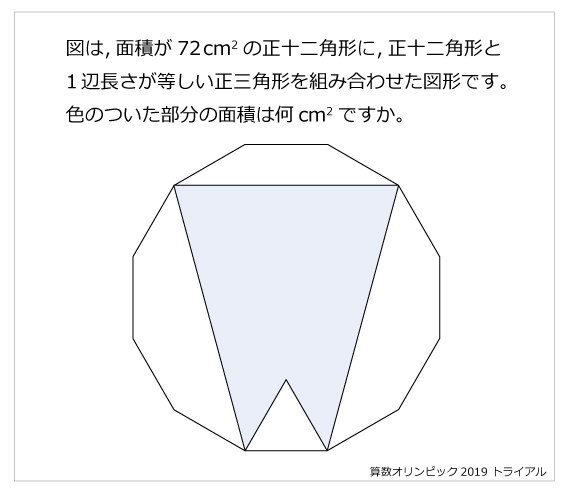



正十二角形 算数星人のweb問題集 中学受験算数の問題に挑戦



正12 角形 ニスヌーピー壁紙




高校数学 正十二角形の周長と面積 多角形の求積の原則 受験の月



正十二边形 搜狗图片搜索



正十二边形 搜狗图片搜索



正十二边形 搜狗图片搜索



正十二边形 搜狗图片搜索




4种方法来求六边形面积




六角形面積公式正六邊形面積公式 百度知道翻譯此網頁 Juliech



图说正十二边形的面积



図形 正十二角形の分解 父ちゃんが教えたるっ




ベスト50 正12 角形 最高のぬりえ
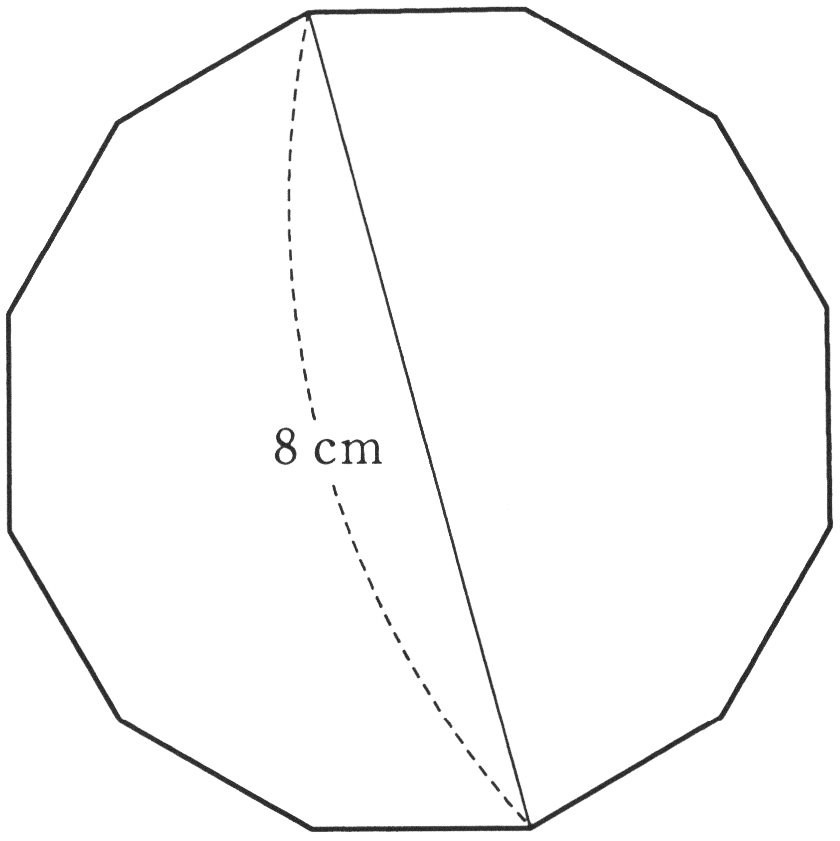



正十二角形の面積 城北19 ジーニアス 中学受験専門塾




正12 角形 ニスヌーピー壁紙



麻布中学校 算数 正十二角形 面積 図形問題 中学受験算数 Youtube



問題187 正十二角形の秘密




4种方法来求六边形面积



問題187 正十二角形の秘密



五边形 维基百科 自由的百科全书




ベスト50 正12 角形 最高のぬりえ




正八邊形 八條長度相等的線段 首尾相連構成的一個封閉形狀的平面圖形叫正八邊形 華人百科



12边形 万图壁纸网



小升初數學考試常考題型和典型題錦集 答案及詳解 雪花新闻




六角非角形十二角形png图片素材免费下载 图片编号 Png素材网




十二边形 Wikiwand




正十二角形の図形問題 仙台市立中等教育学校 年 恋する中高一貫校 適性検査 徹底攻略




如何求正多边形的面积 7 步骤




ベスト50 正12 角形 最高のぬりえ




面積 26 求三角形的 高 的基本題型 Youtube




ベスト50 正12 角形 最高のぬりえ



図形 正十二角形の分解 父ちゃんが教えたるっ


