大熱狂の全国ツアー『Perfume Second Tour 09「直角二等辺三角形TOUR」』 の中から、横浜アリーナ・ツアーファイナル(10月15日)の模様を全曲収録! 三平方の定理(ピタゴラスの定理): ∠ C = 9 0 ∘ \angle C=90^{\circ} ∠ C = 9 0 ∘ であるような直角三角形において, a 2 b 2 = c 2 a^2b^2=c^2 a 2 b 2 = c 2 → 三平方の定理の4通りの三平方の定理 例題 三平方の定理 三平方の定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離) 三平方_折り返し

二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
直角 二 等辺 三角形 定理
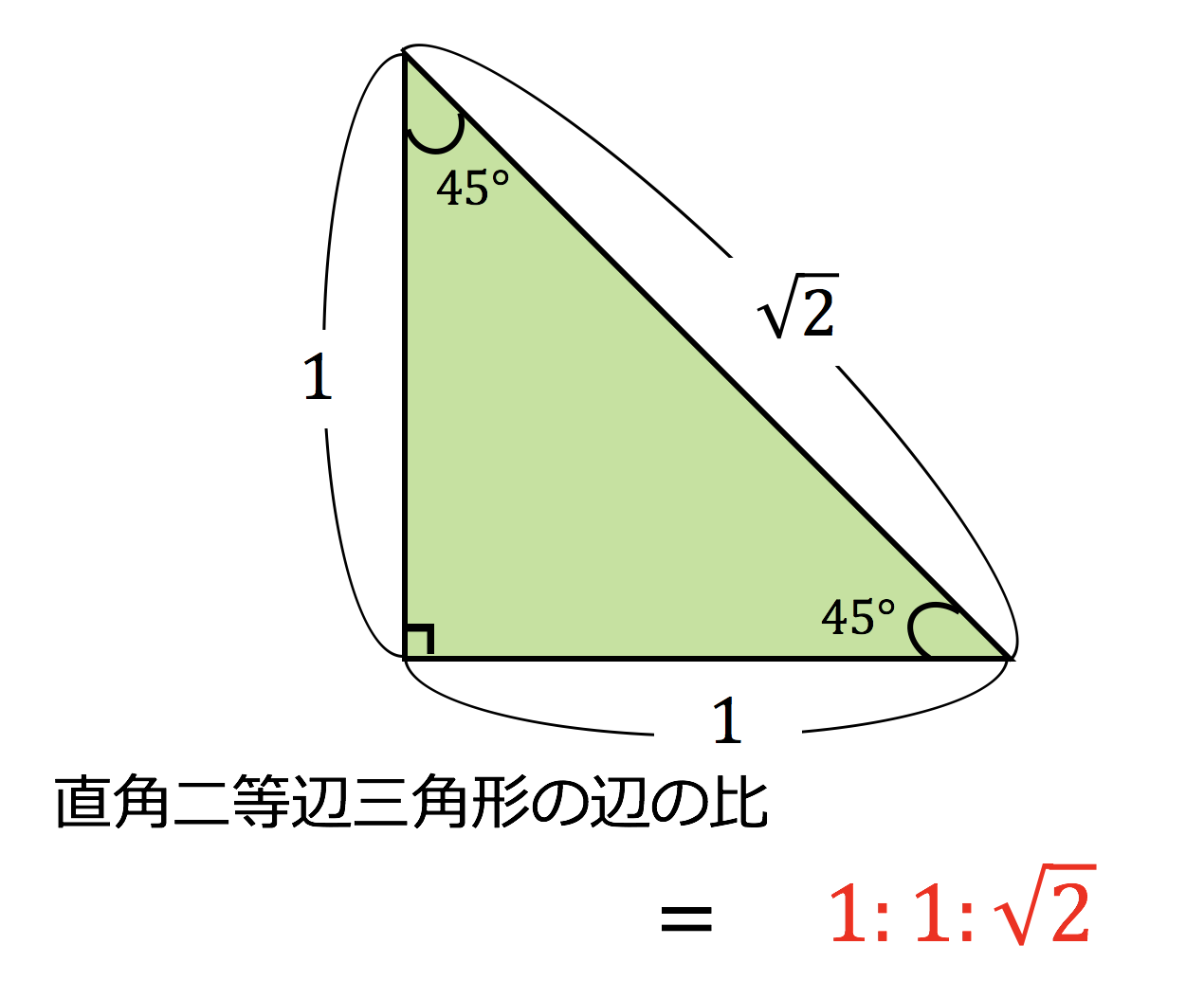
直角 二 等辺 三角形 定理-直角二等辺三角形の辺の比は「三平方の定理」から導くことができます。 直角二等辺三角形の底辺と高さの長さは同じです。 底辺(高さ)の長さを「1」として、三平方の定理に代入すると「斜辺 2 =底辺 2 高さ 2 ⇒ 斜辺 2 =11=2 ⇒ 斜辺=√2」になります。 よって、直角二等辺三角形の辺の比は「1:1;√2」です。 今回は、直角二等辺三角形と三平方の定理との二等辺三角形の定義と定理, 二等辺三角形の定義と定理 二等辺三角形の定義と定理 更新日:15年9月3 日 情報教育係 この情報は滋賀県内教職員にのみ公開されています。 以下のリンクをクリックして限定公開ページを参照してください。 その際には各




なぜ三角形cdeは直角二等辺三角形だとわかるのかが理解できません 教えてください Clear
直角二等辺三角形の定義 は、2つあります。 定義 二等辺三角形の持つ特徴に加え、直角三角形の持つ特徴を併せ持つ図形 3つの角のうち2つの角がそれぞれ である二等辺三角形 1つ目はイメージがしにくいので、2つ目の定義に従って、説明していきます。 すると、直角二等辺三角形は 「3つの角が、、、である三角形」 だとわかります。 図でいうと、下のような直角二等辺三角形(ちょっかくにとうへんさんかくけい、英 isosceles right triangle )は、二等辺三角形の持つ特徴に加え、直角三角形の持つ特徴を併せ持つ図形である。 3つの角のうち2つの角がそれぞれ45°である三角形と定義してもよい。 直角二等辺三角形は二等辺三角形の一つでもあり、直角 この直角三角形は、斜辺以外の 辺が同じ長さなので 直角二等辺三角形 です。
※ よく出てくる特別な三角形なので、 30°・60°・90°の直角三角形 と併せて覚えておいてください ・直角二等辺三角形(45°・45°・90°)の辺の長さの比は、1:1:√2 となる ・1 2 +1 2 = (√2) 2 というような関係を満たしている身近な三平方の定理といえば、小学校からよく使う2つの三角定規です。 直角二等辺三角形の定規の辺の比は、11 √2(内角は、90°、45°、45°) この場合、斜辺が√2です。 1² + 1² =√2²2 特殊な形の三角形で利用される三平方の定理 21 直角二等辺三角形:角度が45°の直角三角形;
まぁ、三平方の定理でも解けますね。 しかし、もし、4ではなく04などの小数や分数が出た場合は、ちょっと計算が苦しくなります。 あくまでも、一時しのぎと考えて使ってください。 本来は、 比を利用するのがベスト です。 Tweet ← 受験数学:三平方直角二等辺三角形 は ピタゴラスの定理 で斜めに上がっている線の実際の寸法がわかる。 立体的に見ると 求めたい斜めの実際の線の長さの2乗=底辺の2乗+高さの2乗 直角三角形で 一番長い辺の2乗=他の短い辺の2乗+他の短い辺の2乗 ピタゴラスの定理 投稿者 okayama_sheet_metal 投稿図形 定義・定理 まとめ 対頂角 𝟖は等しい 直線の角度 ° 平行線の 同位角 𝟖 は等しい 角形の内角の和 °×(𝒏− ) 平行線の 多角形の外角の和錯角 𝟔は等しい ° 同位角 が等しければ、2直線は平行 〇 合同な図形の対応する線分や角は等し い。 錯角 が等しければ、2直線は平行 三角形 四角形



2




各辺の比が決まっている三角形 中学数学 By Okボーイ マナペディア
もくじ 1 三平方の定理の内容:直角三角形と辺の長さの関係 11 分からない辺の長さを計算できる三平方の定理; 直角二等辺三角形の「斜辺だけ」わかってる場合だ。 このとき、 残りの辺はつぎの公式で計算できるよ。 斜辺をb、等しい辺の長さをaとすると、 a = √2b /2 で求められるんだ。 たとえば、 斜辺が4cmの直角二等辺三角形DEFがいたとしよう。 直角二等辺三角形だけど、さっきの計算問題と同じだ。 三平方の定理の公式を使ってやると、 x² = 1² 1² x = √2 になるぞ。 この直角二等辺三角形からピタゴラスは「無理数」を発見したと言われているんだ。




中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
直角二等辺三角形の選択入力値から他の要素の値を計算します。 h = a 2 b = a √ 2 L = ( 1 √ 2 ) a S = a 2 4 h = a 2 b = a 2 L = ( 1 2 ) a S = a 2 4 入力指定直角二等辺三角形の定理 野球場専用のグラウンドを利用するときは、ベースの位置はマーカーがあるので、 ダイヤモンドがすぐできるのですが、小学校の校庭にはマーカーがないので、ゼロからの設置になります。 いつもきれいなダイヤモンド(正四角形)ができないので苦労してました 直角二等辺三角形の中のとある点を求めたい こんばんわ。直角二等辺三角形abcが画像のようにあります。 ad間の距離が m bd間の距離が m cd間の距離が 386m だとし




โน ตของ 確認 三平方の定理 直角二等辺三角形 ช น Senior Clear




メタセコイアの定理 自然数と直角二等辺三角形の面積を繋ぐ無限級数発見 発想力教育研究所 素数誕生のメカニズム
直角二等辺三角形とは?定義・公式・定理や、辺の長さの比 これは直角三角形の角度がそれぞれ、 45 45 90 の奴なんだ。 内角のうちの2つの角度が等しいから、 直角二等辺三角形 ってわけね。 辺の比を使ってやると、三平方の定理を使わずに辺の長さ 赤い部分が二等辺直角三角形になるのはなぜ? 教員採用試験の問題集にあり、恥ずかしながら自分にはわからなかったので質問です。 正方形の中に、正三角形が図のように内接しているとします。 そのとき、赤い三A=b など a=b の→二等辺三角形 a 2 =b 2 c 2 など→ ∠A=90° の直角三角形 などど答えます. (単に「二等辺三角形」と答えると,どの2辺が等しいのか分かりませんので,等しい2辺も書くようにしま




三平方の定理の証明 外接円と直角二等辺三角形を利用した証明 Fukusukeの数学めも




誰か教えてください Clear
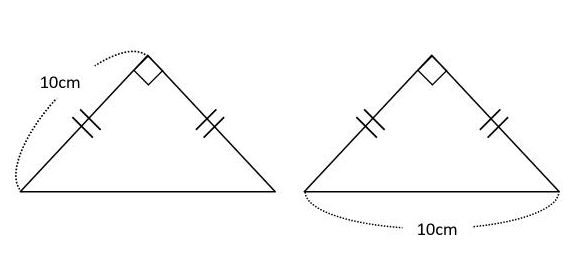
三角形abcはac=cbの二等辺三角形 cdbも二等辺三角形 角a=b=角bcd=15度 ad=10cmのとき、三角形abcの面積を求めよ。 小学校なので、三平方の定理や三角比は使えません。 等積変形や、菱形・平行四辺形にしたり、補助線ひい 台形や二等辺三角形など、普段はあまり口にすることはない言葉です 定理:二等辺三角形の底角は等しい この定理を当然のこととして知っている人も多いと思います。図でも確認しておきましょう。 どこ ダダオ・シャオムの A Piece of Paper HOME ABOUT STUDY CONTACT 数学学習の段階番外編:二等辺三角形の底角の定理 どうもシャオムです。 これまで3回例 (1) 1 2 x 斜辺がxなので 1222=x2 x2 = 5 x > 0 より x= 5 (2) x 12 13 斜辺が13なので x2122



中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン
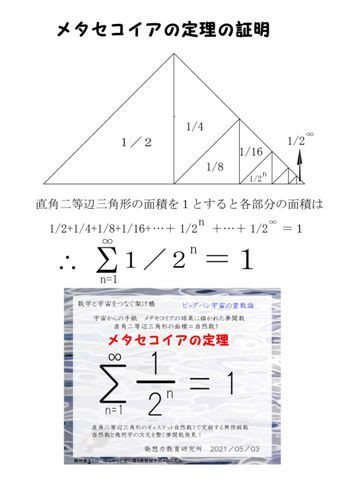



メタセコイアの定理 自然数と直角二等辺三角形の面積を繋ぐ無限級数発見 発想力教育研究所 素数誕生のメカニズム
仮定と結論,逆,合同条件/三角形の合同の証明/二等辺三角形の定理/ 二等辺三角形の性質を使った証明 /二等辺三角形になることを証明/正三角形/ 直角三角形/ 平行四辺形の性質/平行四辺形になるための条件/長方形・ひし形・正方形/ 折り返し /平行線と面積/FdData 入試製品版解答 左の直角三角形は、正三角形を半分にしたものです。 3 3 辺の比は暗記で、 21√3 2 1 3 です。 よって、下の図のように長さが決まります。 x= 3√3 x = 3 3 です。 右の直角三角形は、正方形を半分にした直角二等辺三角形です。 3 3 辺の比は暗記で、 11√2 1 1 2 です。 よって、下の図のように長さが決まります。 y= 3√6 y = 3 6 です。三角形の形状問題(正三角形,二等辺三角形,直角三角形など三角形の種類を言い当てる問題)や証明問題においては,正弦定理や余弦定理を変形して,角度に関する式を辺に関する式に直してから考えるのが原則です. ・ tan A は上記2つを用いてとします



二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係




なぜ三角形cdeは直角二等辺三角形だとわかるのかが理解できません 教えてください Clear
定理 113 二等辺三角形の底角は等しい。 証明 二等辺三角形を (=) とおこう。このとき、bc の中点を x とおく。さて、, について、仮定より =, =, = であるので、三辺相等から合同である。したがって、 = 定理 114 二等辺三角形の頂角から対辺への垂線は、垂直二等分線である。また、頂角の 直角二等辺三角形とは、 二等辺三角形の特徴と直角三角形の特徴をあわせもった三角形 のことです。 直角二等辺三角形の定義 \(3\) つの角のうち、\(2\) つの角がそれぞれ \(45^\circ\) である三角形を「直角二等辺三角形」という。A三平方の定理(ピタゴラスの定理) 直角三角形の直角をはさむ2 辺の長さをa,bとし,斜辺の 長さをcとすると a2 +b2 =c2 が成り立つ。これを三平方の定理(ピタゴラスの定理)という。 直角三角形
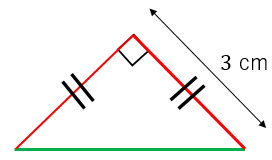



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学



1
定理① 二等辺三角形の底角は等しい。 定理② 二等辺三角形の頂点の二等分線は、底辺を直角に2等分する。 正三角形3辺が等しい三角形(定義) 11√2の特別な三角形は1番長い√2のところが斜辺になります。 また、比(11)からわかるように斜辺でない他の2辺が等しいことからこの三角形は直角二等辺三角形になります。 つまり、90°,45°,45°,の角度を持つ 三平方の定理より、 斜辺をc=√2、他の2辺をa=1,b=1それは、「はしご直角三角形(二等辺 は正三角形を半分にすればできます。 斜辺の中点を中心にすると、円周角(ターレス)の定理に拡張できます。 ここでは、別の視点で拡張してみます。 まず、この三角形には二等辺三角形が二つあります。 斜辺の中点と結べば、どんな直角三角形でも



直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典



直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典
二等辺三角形と定理・定義 ab=acの二等辺三角形で、bd=ceとすれば、∠ade=∠aedであることを証明しなさい。という問題で、 abdと aceの合同を示し、対応する辺が等しいことからad=ae。 adeは二等辺三角形だから 三平方の定理の公式で、直角二等辺三角形は1 今、二等辺三角形が熱い! ~小学校の算数が懐かしい デイリーポータルZ 21年5月31日 自分が小学生時代に流行ったマンガやアニメ、おもちゃなどに触れると、懐かしむのみならず改めてハマってしまうことはないだろうか。 筆者は最近、で中学 中点連結定理、直角、二等辺三角形を利用した問題は、 5月の記事「 少しずつ消化して 」で紹介したように、 今春の大阪府公立入試一般選抜のB問題で出題されました。 「 少しずつ消化して 」の問題は円や三平方の定理が絡んでいて 範囲外なのでやら




高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ



3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ



直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典



見えますか タイルの模様からピタゴラスの定理 Note Board




特別な直角三角形の辺の比 無料で使える中学学習プリント
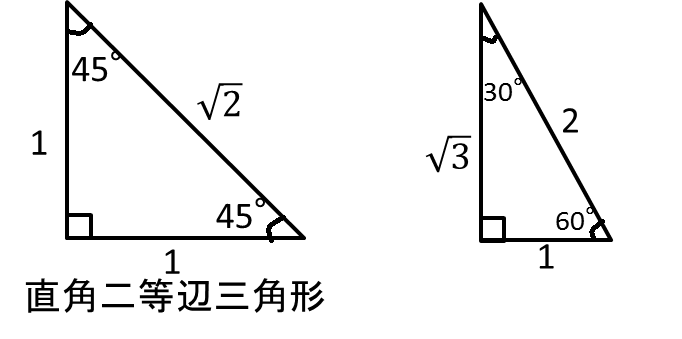



140字で高校受験 数学 三平方の定理 三平方の定理を習ったら 合わせて覚えておこう 三角定規 90 45 45 1 1 2 直角二等辺三角形 90 60 30 1 2 3 2が斜辺 Http T Co Uckznroe5w




ピタゴラスの第2定理発見 三平方根の定理 直角三角形の菅数論の定理 発想力教育研究所 素数誕生のメカニズム



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典



中学三年生 数学の問題です なぜ直角二等辺三角形を半分にす Yahoo 知恵袋




簡単公式 直角二等辺三角形の面積の2つの求め方 Qikeru 学びを楽しくわかりやすく




2 bc Abac Bac90 C E Descubre Como Resolverlo En Qanda




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




二等辺三角形の性質の証明 頂角の二等分線 Youtube




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく




直角二等辺三角形の面積を求める公式は 覚えずに自分でつくろう




3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ




三平方の定理の証明 外接円と直角二等辺三角形を利用した証明 Fukusukeの数学めも




高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ




メタセコイアの定理 自然数と直角二等辺三角形の面積を繋ぐ無限級数発見 発想力教育研究所 素数誕生のメカニズム




2つの直角三角形の角の和 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog




二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者




二等辺三角形になることの証明 Youtube




3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ



直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明




直角三角形の合同条件とその証明 数学fun




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




簡単公式 直角二等辺三角形の面積の2つの求め方 Qikeru 学びを楽しくわかりやすく




中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ Youtube
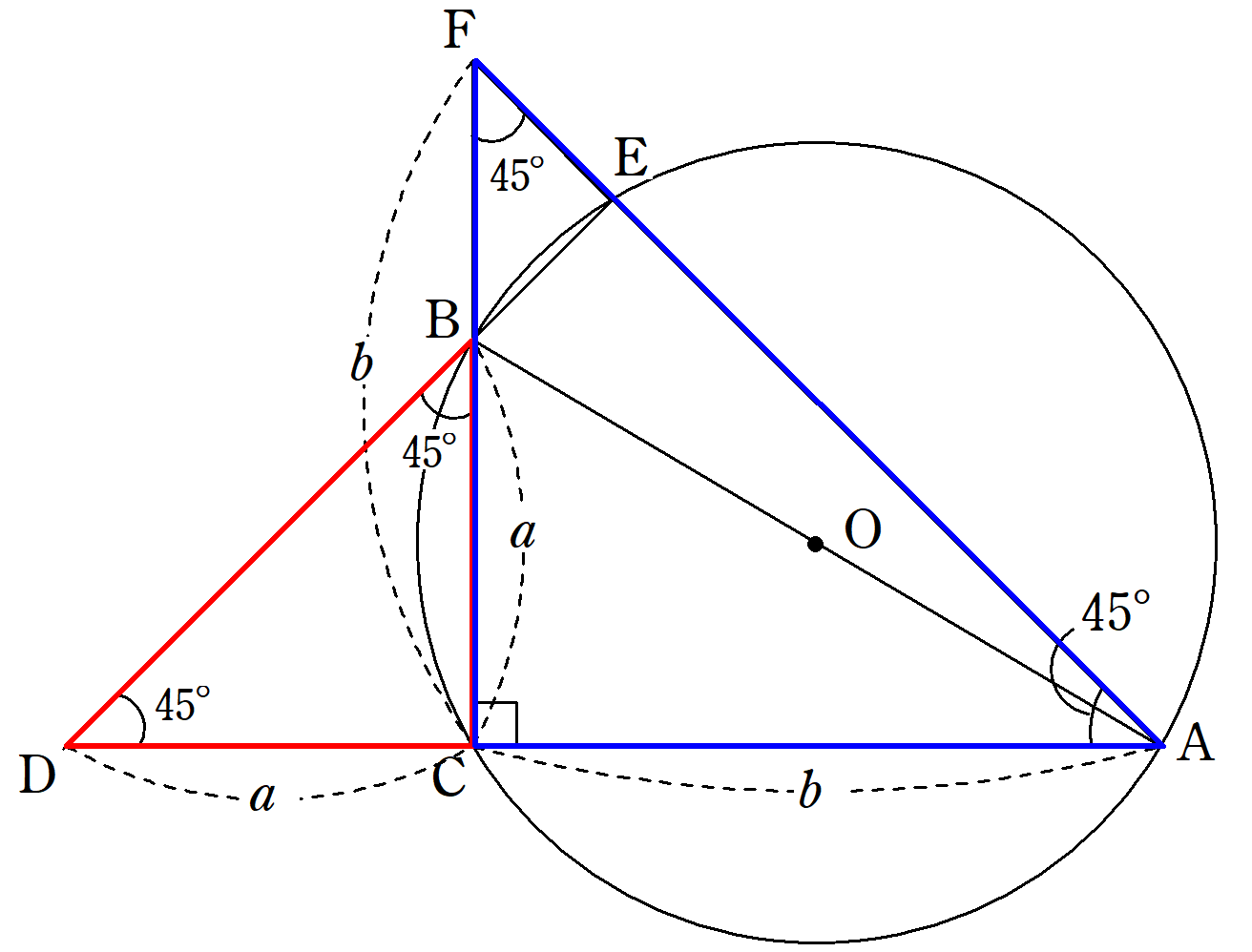



三平方の定理の証明 外接円と直角二等辺三角形を利用した証明 Fukusukeの数学めも




簡単公式 直角二等辺三角形の面積の2つの求め方 Qikeru 学びを楽しくわかりやすく
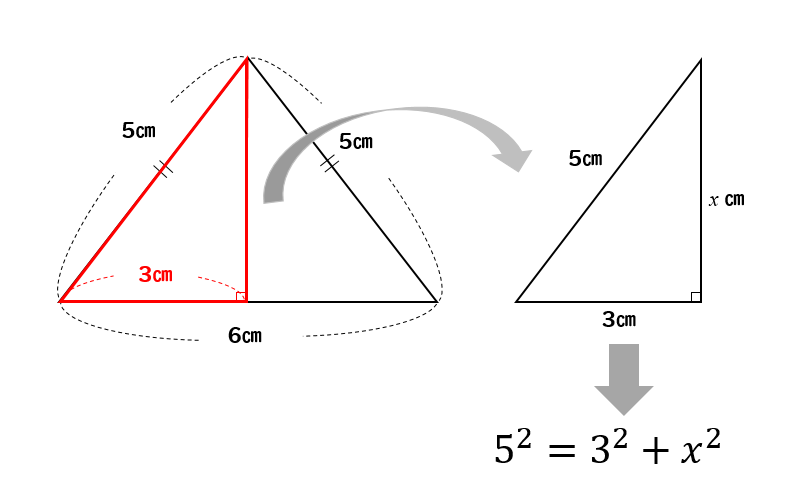



高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ



高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ




二等辺三角形の定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく



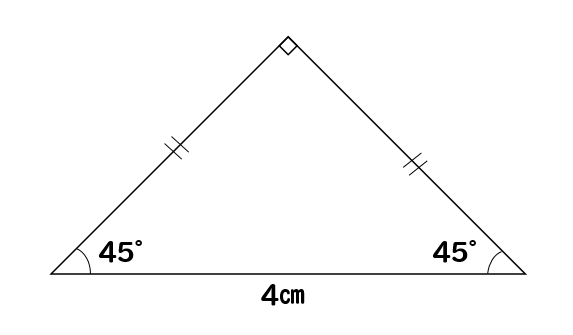
直角二等辺三角形 Wikipedia




簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



高校入試 英語 数学 特別な直角三角形
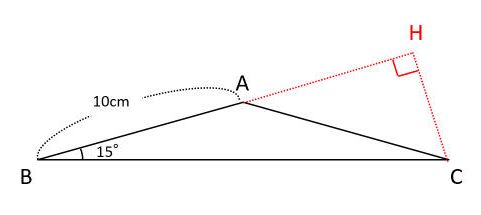



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




直角二等辺三角形の面積を求める公式は 覚えずに自分でつくろう
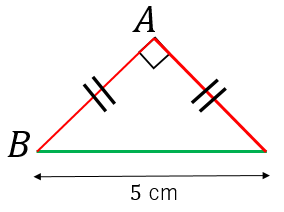



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学




直角三角形の合同条件とその証明 数学fun




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく




の 3 4 が分かりません また と の 1 2 は合っていますか Clear




3 4 5の三角形で 本当に直角ができる Note Board




直角二等辺三角形abcの面積を求めよ 解答編 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog




高校数学 三角形の形状 正三角形 二等辺三角形 直角三角形 受験の月




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比




二等辺三角形 Wikipedia




3 おかしな不等辺三角形 Imujii S Page




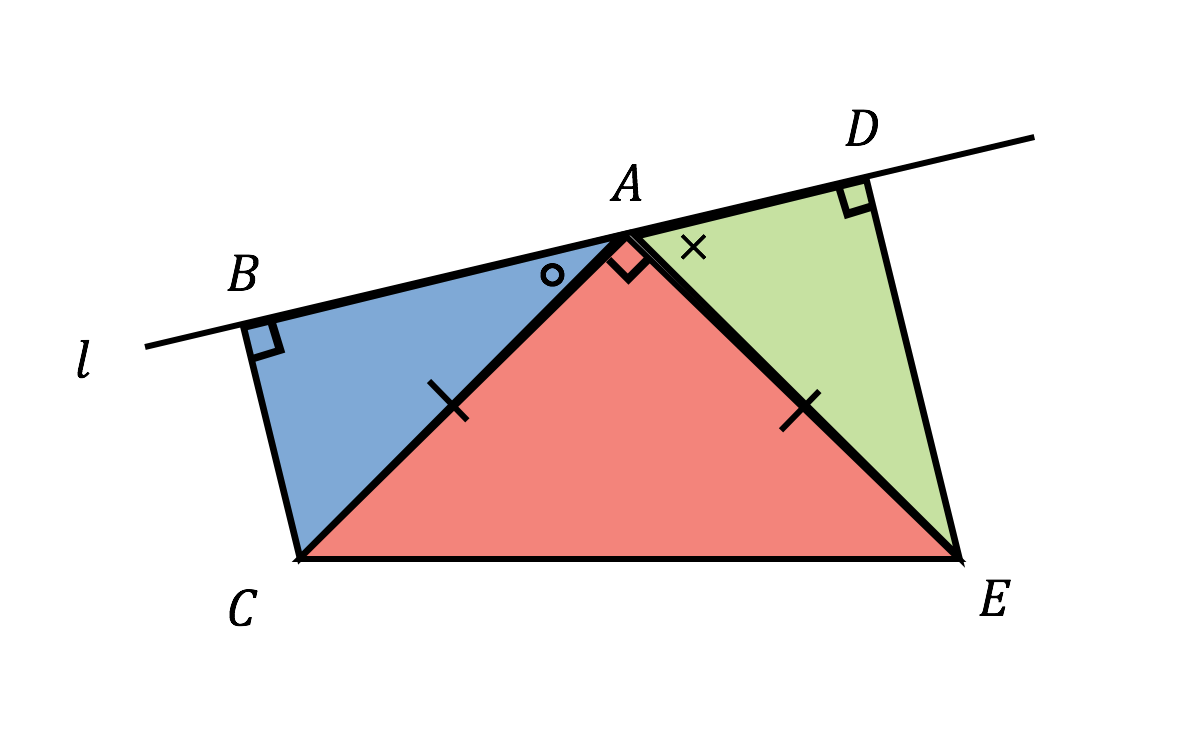
証明の問題なのですがなぜ Adeは直角三角形ではなく直角二等辺三角形となるのでしょう Clear
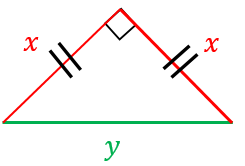



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学




直角三角形
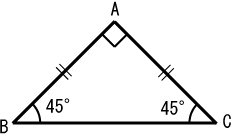



直角二等辺三角形 Wikipedia
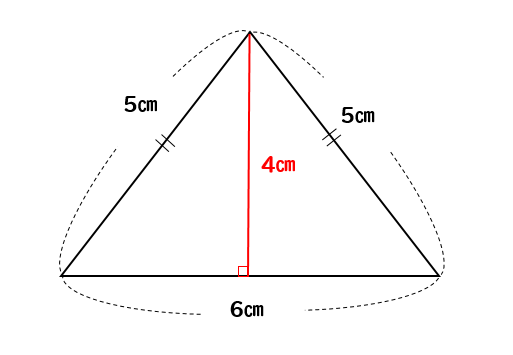



高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット



1




二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者
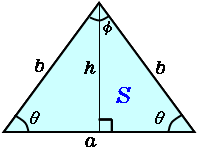



二等辺三角形 高精度計算サイト




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく




30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学
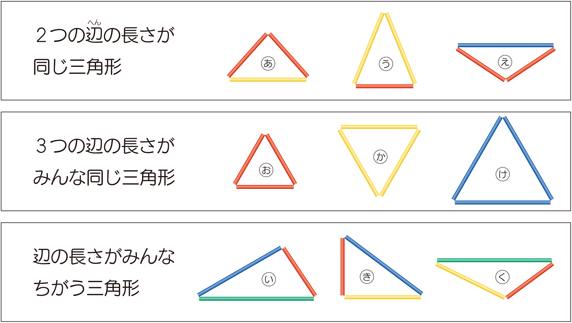



二等辺三角形と正三角形 算数用語集



1




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



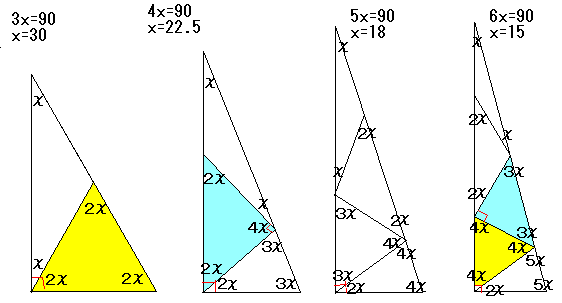
3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ



はしご直角三角形



メタセコイアの定理 自然数と直角二等辺三角形の面積を繋ぐ無限級数発見 発想力教育研究所 素数誕生のメカニズム
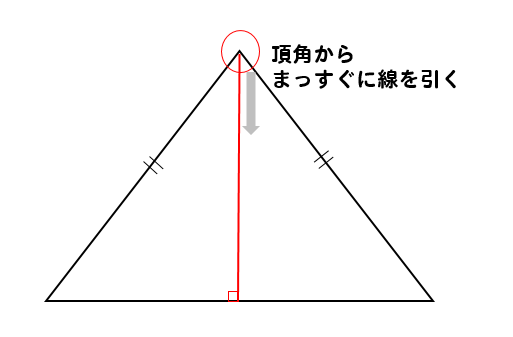



高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ




直角2等辺三角形と平行線 幾何学の証明がわからないので質問します 直 Okwave



直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典




直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学



直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典




数学 中2 64 二等辺三角形 Youtube




世界に1ペアだけ 周りの長さも面積も同じ直角三角形 二等辺三角形 慶大院生ペア証明 朝日新聞デジタル




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学




働きアリ 三平方の定理



直角二等辺三角形と三平方の定理の関係は 3分でわかる計算 公式 辺の比 例題
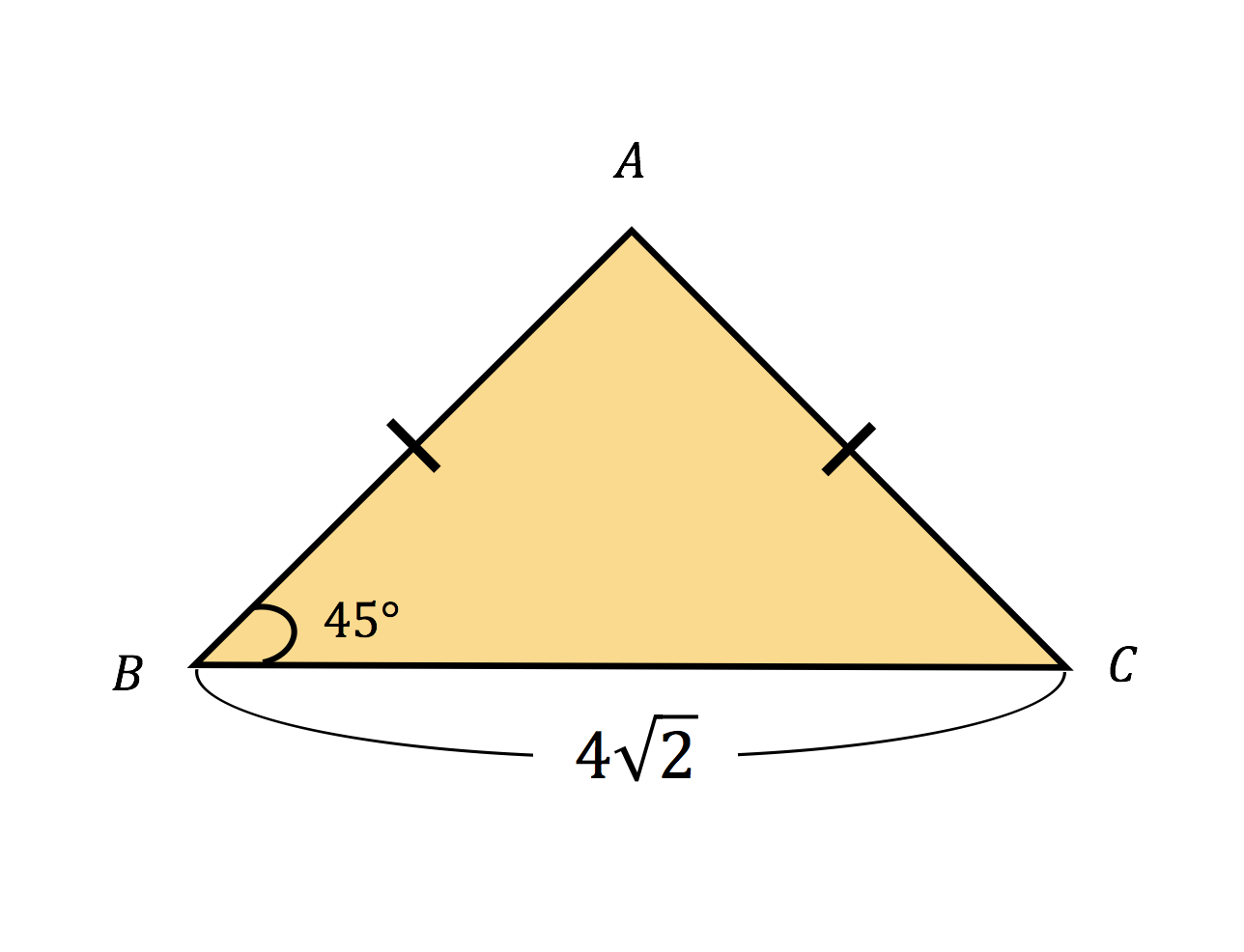



3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ




直角二等辺三角形の辺の求め方 直角二等辺三角形の底辺が106センチメ 数学 教えて Goo




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ



直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典



直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明
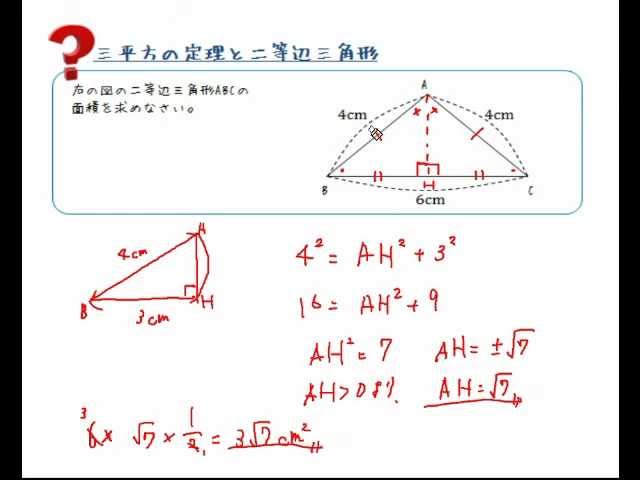



三平方の定理と二等辺三角形 Youtube




名門国立小のカリスマ先生に聞く なんでこれがわからないの でイラっときた時の教え方 Forbes Japan フォーブス ジャパン



3
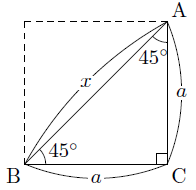



三角定規の3辺の比 まなびの学園




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ



図形の計算問題です 図のように半径2cm 中心角90 の Yahoo 知恵袋


